Drawing Bezier Curves

:: graphics, bezier, dc

This blog post shows to use the racket/draw library to draw Bezier curves.

A Bezier curve connects two points, so we need a way to represent points.

<pt-definition> ::=

(struct pt (x y))

A Bezier curve from p0 to p3 with control points p1 and p2 is represented by a bez structure:

<bez-definition> ::=

(struct bez (p0 p1 p2 p3))

The curve leaves p0 in the direction towards p1. The curve approaches p3 in the direction from p2.

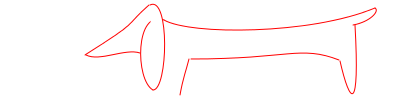
Given these structure definitions we can now represent Picasso’s Dachshund (see Jeremy Kun’s Blog).

<dachshund> ::=
(define dachshund
  (list
   (bez (pt 180 280) (pt 183 263) (pt 186 256) (pt 189 244))
   (bez (pt 191 244) (pt 290 244) (pt 300 230) (pt 339 245))
   (bez (pt 340 246) (pt 350 290) (pt 360 300) (pt 355 210))
   (bez (pt 353 210) (pt 370 207) (pt 380 196) (pt 375 193))
   (bez (pt 375 193) (pt 310 220) (pt 190 220) (pt 164 205))
   (bez (pt 164 205) (pt 135 194) (pt 135 265) (pt 153 275))
   (bez (pt 153 275) (pt 168 275) (pt 170 180) (pt 150 190))
   (bez (pt 149 190) (pt 122 214) (pt 142 204) (pt  85 240))
   (bez (pt  86 240) (pt 100 247) (pt 125 233) (pt 140 238))))

The racket/draw library represents Bezier curves (or rather zero or more closed subpaths and one open subpath) as dc-path% objects. The function bez->dc-path converts the representation of a Bezier curve from a bez structure into dc-path%.

<conversion> ::=
(define (bez->dc-path b)
  (match-define (bez (pt x0 y0) (pt x1 y1) (pt x2 y2) (pt x3 y3)) b)
  (define p (new dc-path%))
  (send p move-to x0 y0)
  (send p curve-to x1 y1 x2 y2 x3 y3)
  p)

It is now trivial to define a function, that draws a Bezier curve using a given drawing context, dc:

<draw-bez> ::=
(define (draw-bez dc b)
  (send dc draw-path (bez->dc-path b)))

The dachshund is drawn piece by piece:

<draw-dachshund> ::=
(define (draw-dachshund dc)
  (for ([b dachshund])
    (draw-bez dc b)))

Using drawing contexts allow to use the same draw-dachshund function to draw the dachshund on pdfs, bitmaps, and, more. Let’s draw the dachshund on a bitmap.

<example> ::=
(define bm (make-object bitmap% 400 100))
(define dc (new bitmap-dc% [bitmap bm]))
(send dc set-smoothing 'smoothed)
(send dc set-pen "red" 1 'solid)
(send dc translate 0 -185)
(draw-dachshund dc)
bm

To run the code in this blog post, the pieces must be assembled in this order.

<*> ::=
(require racket racket/draw)
(provide bm)
<pt-definition>
<bez-definition>
<dachshund>
<conversion>
<draw-bez>
<draw-dachshund>
<example>

image

Summer Project: Meta(font|post) in Racket

:: graphics, hobby, metafont, metapost, tikz

The summer holiday is getting closer. This means there is time to focus on hacking. Last year my summer project was to implement a matrix library and a number theory library.

This year I have decided to write a graphics library inspired by the approach taken by Metafont, Metapost and Tikz. The basic concept in these libraries is a path. The existing Racket library pict on the other hand is based on pictures.

Bezier curves will be used to draw the paths. Drawing a Bezier curve is straight forward; the builtin graphics library, racket/draw has support for this in the form of curve-to.

What is needed is convenient ways of specifying and manipulating paths.

The first problem will be this: Given points P0, P3, P6, ..., Pn. Draw a "pretty" curve through these points. That is, determine which Bezier curves is to be drawn between P0 and P3, between P3 and P6 etc.

John D. Hobby and Donald Knuth introduced the algorithm now known as "Hobby’s Algorithm" in Metafont to solve this problem. It is the central algorithm of the library.

The second problem is to introduce syntax for specifying paths. There is no doubt that the popularity of MetaPost in TeX circles is the concise syntax - so I’ll see how much it makes sense to steal.

The third problem is to support for specifying points based on linear equations. Luckily the grunt works is already done - the matrix library contains equation solvers.

Breaking large project into chunks help tremendously. Just witness how fast the number of completed Racket tasks went up on RosettaCode.

  1. Draw a Bezier curve using racket/draw

  2. Explain Hobby’s algorithm

  3. Implement Hobby’s algorithm

  4. Design syntax for paths

  5. Implement syntax for paths

  6. Document syntax for paths

  7. Predefinitions for standard paths

  8. Examples - inspration from the Metafontbook and Tikz

  9. Linear expressions and "linear variables"

  10. Syntax for linear expressions and linear variables.

  11. From fonts to paths

  12. Higher order path operations

  13. Bounding boxes for paths

  14. Intersections between curves

  15. Coloration of areas

  16. Bitmaps

  17. Relation to picts?